引言

指数衰减方程是许多化学和生物过程的模型。当某一事物的发生率与剩余量成正比时，就会用到它。以下是三个本示例：

•当配体与受体解离时，在任何短时间间隔内解离的分子数与该时间间隔开始时结合的分子数成正比。等效地，与受体结合的每个配体分子都有一定的概率在任何小时间间隔内从受体解离。这种概率不会随着配体在受体上停留时间的延长而增加。

•当放射性同位素发生衰变时，在任何短时间间隔内发生衰变的原子数与在时间间隔开始时存在的未衰变原子数成正比。这意味着，每个原子在一小段时间间隔内衰变的概率是一定的，而且这个概率是恒定的。任何特定原子衰变的概率都不会随时间而改变。由于未衰变原子的数量越来越少，因此样本的总衰变量会随着时间的推移而减少。

•当药物由肝脏代谢或由肾脏排泄时，代谢或排泄的速度通常与血浆中的药物浓度成正比。每个药物分子都有一定的概率在一小段时间内被代谢或分泌。随着药物浓度的降低，其代谢或排泄率也会随之降低。

输入数据

创建 XY 数据表。在 X 列中输入时间，在 Y 列中输入反应（结合力、浓度......）。如果有多个实验条件，则将第一个条件放入 A 列，第二个条件放入 B 列，等等。

您还可以选择指数衰减的样本数据集。

输入数据后，点击分析，选择非线性回归，选择指数方程面板，然后选择单相衰减。

考虑将高原限制为常数零值

在这种情况下，应将参数 Plateau 约束为等于零的常数。为此，请转到非线性回归对话框的 "约束"选项卡，将 Plateau 旁边的下拉菜单设置为 "等于常数"，然后输入 0.0。

模型

Y=(Y0 - 高原)*exp(-K*X) + 高原

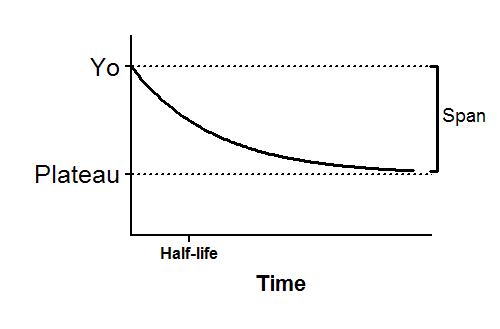
Y0是 X（时间）为零时的 Y 值。其单位与 Y 相同、

Plateau是无限时间时的 Y 值，单位与 Y 相同。

K是速率常数，用 X 轴时间单位的倒数表示。如果 X 以分钟为单位，则 K 以倒数分钟为单位。

Tau是时间常数，单位与 X 轴相同。它是以 K 的倒数来计算的。

半衰期以 X 轴的时间单位表示。计算公式为 ln(2)/K。

跨度是 Y0 和高原之间的差值，单位与 Y 值相同。

 

指数衰减的导数等于-K*Y。因此，初始速率等于-K*Y0。