在拟合对数(剂量)与反应曲线之前,通常要先对数据进行归一化处理。本页解释了为什么在这种情况下不应该使用加权回归。
对非标准化数据进行加权拟合 -- 效果很好
下图显示了一种常见情况的模拟数据。当 Y 值较大时,重复数据之间的散度较大。事实上,这些数据是模拟出来的,因此样本间的 SD 与 Y 值成正比。
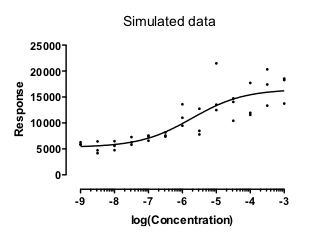
使用相对权重法可以很好地拟合这些数据。这可以使点与曲线之间相对距离的平方和最小化。换句话说,就是最小化:
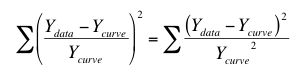
我进行了 10,000 次模拟,发现在每种情况下,拟合效果都很好,并给出了合理的答案(EC50 在数据范围内)。到目前为止,这并不奇怪。数据拟合假设的模型与模拟数据所用的方法完全一致,而且这些拟合效果很好。
对归一化数据的加权拟合 -- 唉
人们通常喜欢将剂量反应数据归一化,这样 Y 值的范围就从 0% 到 100% 不等。 如果用加权非线性回归拟合这些归一化数据,会发生什么情况?
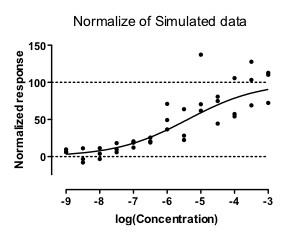
我通过模拟回答了这个问题。在 1000 个模拟数据集中,有 223 个根本无法拟合。此外,60 个模拟数据集给出了无稽之谈的结果,EC50 超出了数据的范围。其余 72% 的模拟结果看起来还可以,但有些模拟结果的置信区间非常宽。
这是怎么回事?
在未归一化的数据中,X=-4 时拟合优度曲线的 Y 值是 X=-8 时曲线 Y 值的 3.05 倍。由于权重与曲线 Y 值的平方成正比,因此靠近曲线顶部(X=-4 处)的点所占权重是靠近曲线底部(X=-8 处)的点所占权重的 3.052或 9.28 倍。
归一化数据的情况则截然不同。 在第一个模拟数据集中,X=-4 处拟合优度曲线的 Y 值是 X=-8 处曲线 Y 值的 17.77 倍。由于权重与曲线 Y 值的平方成正比,因此靠近曲线顶部(X=-4 处)的点的权重是靠近曲线底部(X=-8 处)点的权重的 17.772或 315.8 倍。由于曲线顶部的点比底部的点获得的权重大得多,底部的点基本上就被忽略了,导致整个曲线拟合效果不佳。
还有一个问题。归一化数据集底部附近的一些 Y 值是负值。当有些值是负值,有些值是正值时,加权因子真的一点意义都没有。
总之:归一化后,重复样本间的 SD 不再与 Y 值成正比,因此相对权重并不合适。
小结
加权非线性回归的整体思路是使回归所使用的加权方案与实际数据的变化相匹配。如果对数据进行归一化处理,通常的加权方案都不能很好地发挥作用。
如果您真的想在一个从 0% 到 100% 的归一化坐标轴上显示您的数据,您可以这样做。首先使用适当的加权方案将模型与实际数据拟合。然后对数据和曲线进行归一化处理。