样本的SD与总体的SD不同

从数值样本中计算标准偏差很简单。但标准偏差有多精确呢？您可能碰巧获得了一些紧密相连的数据，从而使标准差偏低。或者，您可能碰巧获得了比总体更分散的数据，从而使标准差偏高。样本的 SD 值可能不等于甚至接近总体的 SD 值。

标差的 95% CI

您可以用 95% 置信区间 (CI) 来表示任何计算值的精度。这种方法并不常见，但计算一个标样的置信区间肯定是可行的。我们将在解释平均数 CI 的下一节中更多地讨论置信区间。这里我们讨论的是标差的 CI，两者截然不同。

解读标差的 CI 非常简单。您必须假设您的数据是从高斯分布中随机独立抽样得到的。您从这一个样本中计算出 SD 及其 CI，然后用它来推断整个人群的 SD。您可以 95% 地确定 SD 的 CI 包含人口的真实总体标准偏差。

自变量的 CI 有多宽？答案当然依赖于样本量（N），如下表所示。

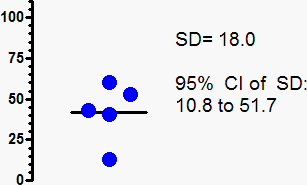
根据上图所示的五个数值计算出的标准偏差为 18.0。但是，从这些数值中抽取的总体的真实标准偏差可能相差很大。由于 N=5，95% 置信区间从 10.8 (0.60*18.0) 扩展到 51.7 (2.87*18.0)。如果只用 5 个值来计算 SD，那么 SD 的 95% 置信区间上限几乎是下限的 5 倍。

大多数人都对小样本能如此准确地定义标中值感到惊讶。随机抽样会对小数据集产生巨大影响，导致计算出的标准偏差与真实的总体标准偏差相差甚远。

请注意，置信区间并不对称。为什么？因为标准差总是正数，所以置信区间下限不能小于零。这意味着置信区间上限在样本标准差之上的延伸通常比下限在样本标准差之下的延伸更远。对于小样本，这种不对称性非常明显。

如果您想自己计算这些置信区间，请使用这些 Excel 公式（N 为样本量；95% 置信度的 alpha 为 0.05，99% 置信度的 alpha 为 0.01，等等）：

下限：=SD*SQRT((N-1)/CHIINV((alpha/2), N-1))

上限：=SD*SQRT((N-1)/CHIINV(1-(alpha/2), N-1))