在一叠数据中识别异常值很简单。单击列数据表中的分析，然后从列数据分析列表中选择识别异常值。Prism 可以对数据集中少至三个值执行异常值检验。

注意：本页介绍如何从列数据设置数据表格式的数值堆中识别异常值。Prism 还可以在非线性回归过程中识别异常值。

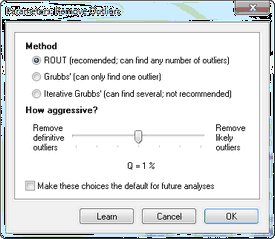
哪种方法？

Prism 提供三种识别异常值的方法：

ROUT

我们开发了ROUT 方法，用于在使用非线性回归拟合曲线时检测异常值。Prism 将此方法调整为从列数据表中的一叠值中检测异常值。ROUT 方法可以识别一个或多个异常值。

格拉布斯方法

Grubbs 检验法可能是识别异常值最常用的方法。这种方法也称为 ESD 方法（极端学生化偏差）。它只能在每个数据集中识别出一个异常值。Prism 使用双侧格拉布斯检验，这意味着它会检测出一个比其他值大很多的值，或者一个比其他值小很多的值。

迭代格拉布斯检验

虽然格拉布斯方法是为检测一个异常值而设计的，但它经常被扩展用于检测多个异常值。这种方法很简单。如果发现一个异常值，就将其删除，然后再次用格拉布斯检验法检验剩余的值。如果第二次检验发现异常值，则删除该值，并进行第三次检验......

虽然格拉布检验能很好地找出数据集中的一个异常值，但对于多个异常值就不太适用了。在一个小的数据集中，第二个异常值的存在会阻止第一个异常值被检测出来。这就是所谓的掩蔽。 格拉布斯的方法是通过计算值与平均值之间的差值，然后用这个差值除以所有值的标准偏差来识别异常值。当该比率过大时，该值就被定义为异常值。问题在于，标准偏差是根据包括异常值在内的所有值计算出来的。如果有两个异常值，标准偏差就会变得很大，从而使该比率降低到用于定义异常值的临界值以下。查看屏蔽本示例。

建议

•如果以某种方式确定数据集没有异常值或只有一个异常值，则选择格拉布斯检验。

•如果要考虑异常值不止一个的可能性，则选择 ROUT 方法。比较 Grubbs 方法和 ROUT 方法。

•避免使用格拉布斯迭代法。

•用 Prism 创建盒须图时，可以选择显示 Tukey whiskers，当点与中位数的距离超过四分位数间距（第 75 个百分位数与第 25 个百分位数之差）的 1.5 倍时，就可以单独显示。我们没有在 Prism 中实现这种异常值检测方法（除了创建盒须图之外），因为它似乎没有被广泛使用，也没有真正的理论基础。如果您希望我们加入这种异常值检测方法，请告诉我们。

有多严重？

没有办法从高斯分布的采样值中干净地分离出异常值。总是有可能遗漏一些真正的异常值，也有可能将一些 "好点 "错误地识别为异常值。你需要决定如何积极地定义异常值。根据你选择的异常值检测方法的不同，选择也有些不同。

格拉布斯检验。选择α。

使用格拉布斯检验时，需要指定阿尔法。它的解读与任何统计学显著性检验相似。如果没有异常值，α 就是错误识别异常值的几率。

请注意，alpha 适用于整个实验，而不是每个值。假设将 alpha 设为 5%，检验一个包含 1000 个值的数据集，所有值都从高斯分布中采样。最极端值有 5%的几率被识别为异常值。这 5%适用于整个数据集，无论它有多少个值。如果用 5%乘以 1000 个样本量，得出的结论是预计会有 50 个异常值被识别出来，那就大错特错了。

Alpha 是双尾的，因为 Prism 中的格拉布斯检验可以识别 "过大 "或 "过小 "的异常值。

常规方法。选择 Q。

ROUT 方法基于错误发现率 (FDR)，因此要指定 Q，即所需的最大 FDR。

当没有异常值（且分布为高斯分布）时，Q 可以像 alpha 一样解读。当所有数据都从高斯分布中采样时（因此不存在异常值），Q 就是识别出一个或多个异常值的几率。

当数据中存在异常值时，Q 就是期望的最大错误发现率。如果将 Q 设为 1%，那么目标是不超过 1%的已识别异常值是错误的（实际上只是高斯分布的尾部），因此至少 99% 的已识别异常值实际上是异常值（来自不同的分布）。如果将 Q 值设为 5%，则期望识别出的异常值中虚假值不超过 5%，至少 95% 识别出的异常值是真实的。

建议

权衡利弊是显而易见的。如果将 alpha 或 Q 值设得过高，那么许多已识别的 "异常值"实际上就是从与其他数据相同的高斯分布中采样的数据集。如果阿尔法或 Q 值设得太低，则无法识别所有异常值。

异常值的识别没有标准。我们建议您先将 Q 值设置为 1%，或将 alpha 值设置为 0.01。

Prism 如何显示结果

结果显示在三页纸上：

•清理后的数据（异常值已去除）。您可以将此页面作为其他分析的输入，如 t 检验或单向方差分析。

•仅异常值。

•摘要。本页列出每个数据集中检测到的异常值数量。