"检验力"究竟意味着什么？

在进行实验时，您通常对测量某种效应感兴趣：药物处理组的蛋白质浓度是否与对照组不同；与野生型相比，基因敲除株的中位存活时间是否更长；不同处理组之间的基因表达是否不同？

您的实验使用不同人群的样本来收集数据并进行统计分析。这样做的目的是，如果您所寻找的效应确实存在于群体中，那么您就可以（希望）在样本中观察到这种效应。然而，人群内部存在变异性，您不可能总是确定您从更广泛的人群中选取的样本能够让您检测到目标效应。

简而言之，使用经典假设检验方法进行分析时，首先要提出一个 "没有效应"的零假设和一个 "有效应"的替代分析假设。在上述情况中，我们假设人群中确实存在效应。但仅凭偶然性，您所选样本中产生的数据并没有反映出这种效应。换句话说，您的数据得出的 P 值可能大于 0.05（或您作为统计阈值使用的任何 alpha 值）。正因为如此，即使在您取样的人群中确实存在效应，您也不会拒绝零假设（即不存在效应）！

"统计功效"是指当零假设为假时，您拒绝零假设的概率。另一种说法是，统计功效是指当您所寻找的效应存在于人群中时，您拒绝零假设的概率。再想一想我们的本示例：我们一开始就说，效应确实存在于种群中，但由于种群的变异性以及从这些种群中随机抽样，我们可能观察到效应，也可能观察不到。统计功效告诉我们观察到效应的概率是多少，它依赖于很多因素，包括效应在种群中的量，我们从种群中抽取的样本量，以及种群内部的变异性。

统计功效的另一种思考方式：进行无限实验

假设我们在用 t 检验比较两个均值，而且两个群体的均值确实相差很大。我们首先从两个相关人群中收集样本，测量样本均值，进行 t 检验，然后得到 P 值。由于样本的变异性，这个 P 值可能大于 alpha（通常为 0.05），也可能小于 alpha。

但现在，让我们假设从人群中选取新的样本，再次进行游程检验。由于变异性和抽样的原因，样本值会略有不同，t 检验的结果也会不同。我们将从新的检验中得到不同的 P 值，它（同样）可能大于或小于 alpha。

现在，让我们假设我们不断重复这个过程。一些计算出的 P 值将小于 alpha，我们将拒绝零假设，而另一些计算出的 P 值将大于 alpha，我们不会拒绝零假设。我们首先要说明的是，种群均值存在差异，因此如果我们进行相同的实验（从相同的种群中抽取相同样本量的样本），那么我们就会得到一定比例的实验的 P 值小于我们的阈值。如果实验重复无数次，那么 P 值小于临界值的实验百分比就是实验的统计功效。

需要注意的是，这在现实生活中是做不到的，原因有以下几点：

1.我们没有时间或资源进行无限多的实验

2.更重要的是，我们不知道取样人群中是否真的存在这种效应。如果我们已经知道存在效应，那么进行这些实验就没有什么意义了！

统计功效（和贝塔值）的更多技术定义

通常情况下，当您从一个群体中抽取样本时，您的目标是从中确定一些统计对象（平均值、标准偏差等）。另一种统计量可能是两个样本平均值之间的差值。还有一种统计量可能是样本平均值的差除以两个样本的集合标准偏差。最后一种统计量实际上就是 t 检验中使用的 t 统计量。

无论您计算的是哪种统计量，该统计量都会有一个可能的取值范围，这是因为您是从一个更大的群体中抽取样本，而这个群体具有变异性。如果你抽取了许多不同的样本，几乎肯定会得到许多不同的统计量值。这个统计值的分布是由一种叫做 "抽样分布"的东西给出的。在研究统计量以确定不同人群之间是否存在预测效应时，统计量可能取值的分布也在很大程度上依赖于该效应是否真正存在。

幸运的是，只要有足够多的关于人群和预测效应的信息，就有可能在假设效应确实存在和假设效应不存在的情况下，构建统计的抽样分布。我们来看一个 t 统计量的本示例：

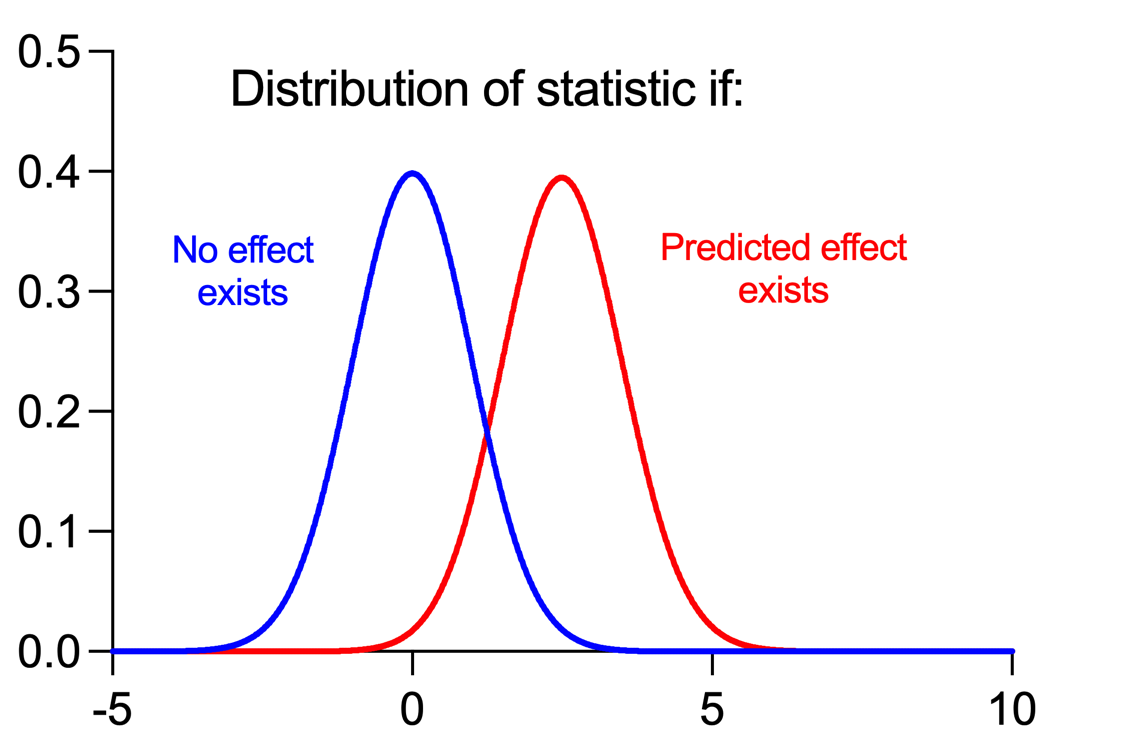
蓝色曲线是假设不存在影响的抽样分布。请注意，该分布以零为中心，如果不存在影响，这是有道理的。然而，由于种群的变异性以及从种群中抽取样本的事实，即使不存在影响，也仍有可能得到大于或小于零的 t 统计量。

红色曲线是假设特异性预测效应确实存在的抽样分布。在这种情况下，分布的中心约为 2.5。这是由于如果存在预测效应，那么确定的 t 统计量离零更远的概率要大得多（但并非不可能为零）。

当您通过从这些人群中抽取样本并计算 t 统计量来进行实验时，您会将该 t 统计量与一个 "临界值"进行比较，以确定您所获得的结果在统计学上是否显著。这可以用这些曲线直观地表示出来。下面是零假设（蓝色曲线，不存在影响）的抽样分布以及临界 t 值（垂直线）：

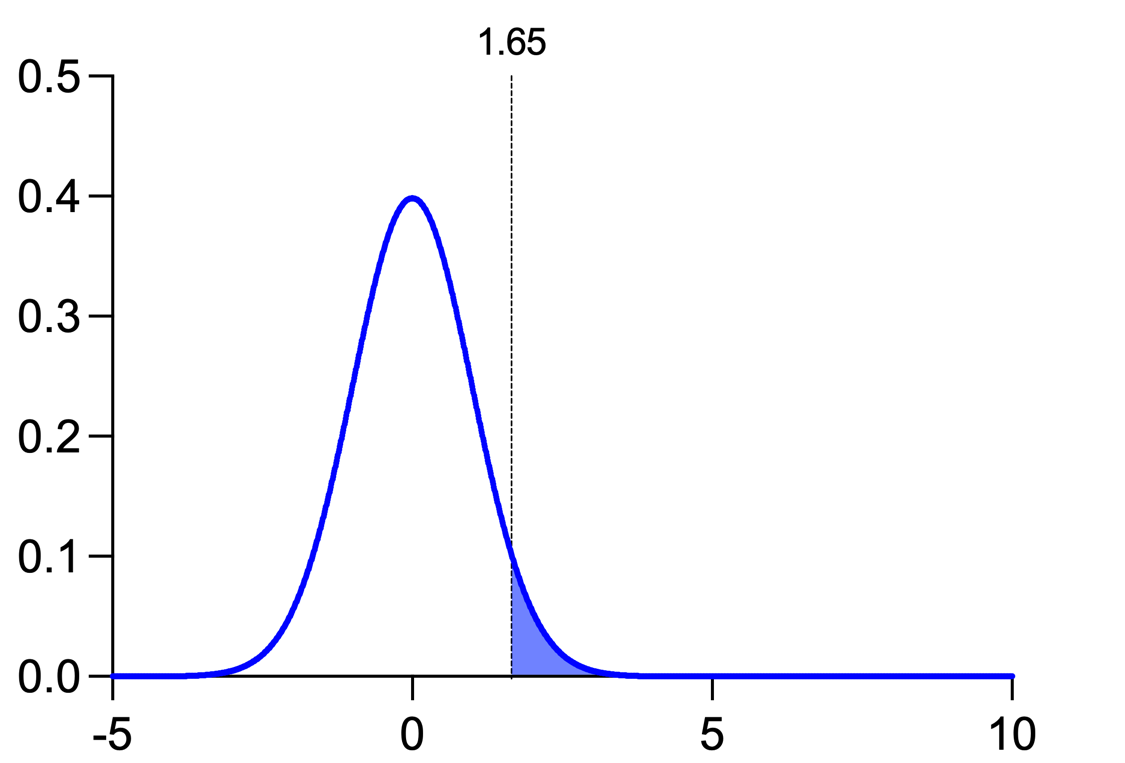
阴影区域表示如果零假设成立，t 统计值大于临界值的概率。在本例中，阴影区域代表该曲线下总面积的 5%。这代表了 alpha 的概念，即当零假设实际为真时拒绝零假设的概率。如果使用不同的 alpha 值，就会得到不同的临界值，最终阴影区域内的曲线面积也会不同。

同样，临界值也可以与红色曲线结合使用：

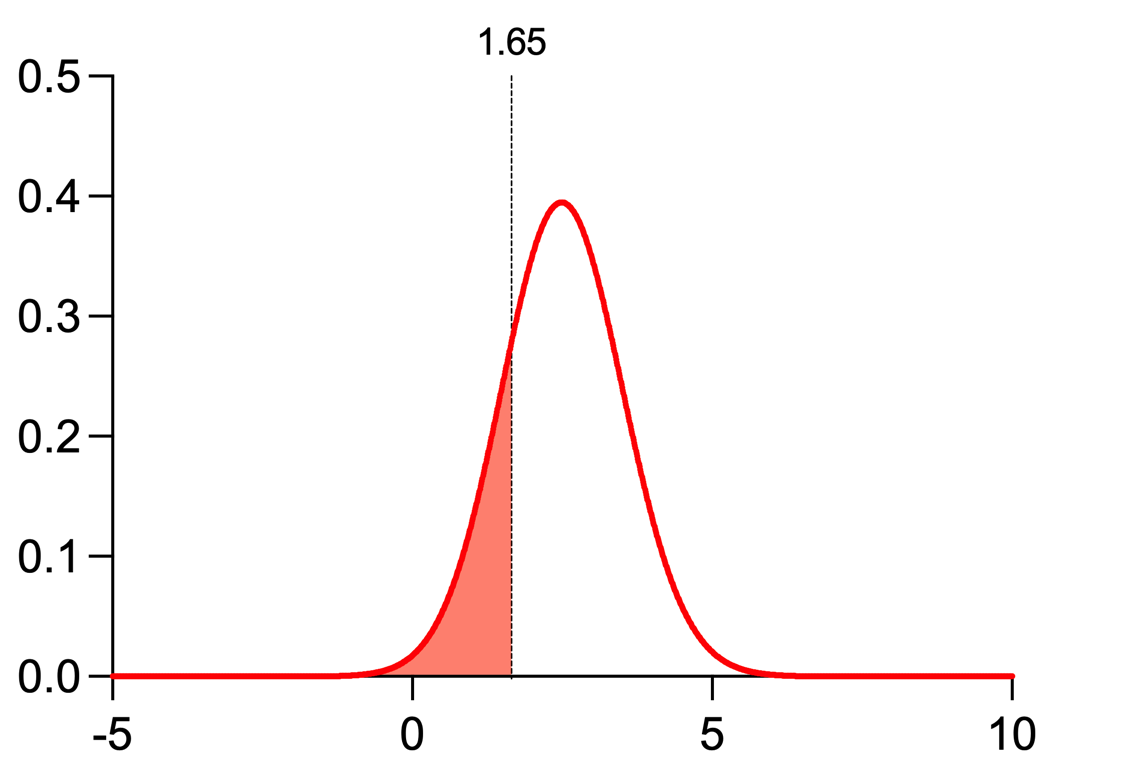
在这种情况下，阴影区域代表在替代假设为真的情况下，t 统计值小于临界值的概率。在这里，阴影区域代表该曲线下总面积的 20%。这是贝塔概念的表示，即当零假设为假时，未能拒绝零假设的概率（第二类错误）。换句话说，它是在效应实际存在时未能检测到效应的概率。您可能会注意到，α（发生 I 型错误的概率）比β（发生 II 型错误的概率）小 4 倍，而这两个值都很常见。一种思考方式是，使用这些值意味着避免 I 型错误（假阳性）比 II 型错误（假阴性）重要 4 倍。

统计功效实际上是由β直接导出的：

统计功效 = 1 - β

因此，在上面的本示例中，β 值为 0.20，统计功效等于 0.8 或 80%。与阿尔法和 0.05 值一样，这只是统计功效的常用值，并不是严格要求。归根结底，作为研究者，您应该决定在设计实验时希望达到什么样的统计功效值。下一节将对此进行更详细的讨论。

把上面的图片和信息放在一起，我们可以得到以下结果：

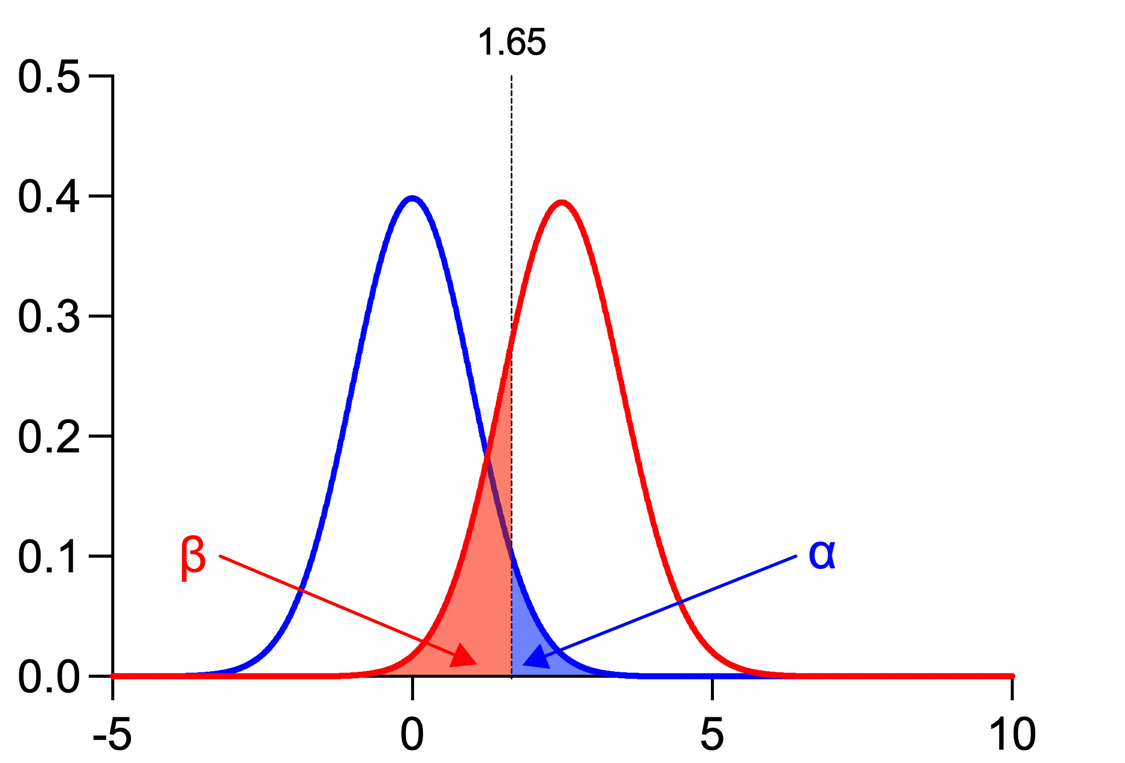
•α（α）：I 类错误的概率（在零假设为真的情况下拒绝零假设，即 "假阳性"），通常为 0.05 或 5%

•贝塔 (β)：第二类错误概率（当零假设为假时不拒绝零假设，即 "假阴性"），通常为 0.2 或 20

•统计功效 (1-β)：当零假设为假时（当效应真实存在时）拒绝零假设的概率，通常为 0.8 或 80%。

我需要多少统计功效？

统计功效是指假设所研究的效应在抽样人群中真实存在，那么实验从您的样本中得出 "统计学显著"结果的几率。您需要多少统计功效？这些指导原则可能有用：

•如果一项实验的统计功效小于 50%，那么只有在一半的实验中存在目标效应，您才能检测到目标效应。这种统计功效的研究确实没有多大帮助，而且（可能更糟的是）不太可能具有可重复性

•许多研究者在选择样本量时，都希望获得 80% 的统计功效。这是任意的，但常用

•理想情况下，统计功效的选择应依赖于发生II 类错误的后果。

使用 Prism 进行统计功效分析

统计功效分析（和样本量计算）可通过 Prism Cloud 针对各种实验设计进行。