PC 分数图直观地展示了 PCA 所实现的维度缩减。定义 PC 后，利用定义每个 PC 的线性组合计算每个 PC 的得分。本示例中，定义 PC1 和 PC2 的线性组合如下（系数由 PC1 和 PC2 的特征向量获得）：

PC1 = 0.552*（变异性 A）+ 0.553*（变异性 B）- 0.227*（变异性 C）+ 0.181*（变异性 D）- 0.530*（变异性 E）

PC2 = -0.246*（变异性 A）- 0.094*（变异性 B）- 0.634*（变异性 C）+ 0.694*（变异性 D）+ 0.215*（变异性 E）

将每个变异性的标准化数据值输入这些公式，就会生成 PC 分数表。如果我们将 PC1 和 PC2 分别绘制在横轴和纵轴上，就会得到下图，其中每个点代表原始数据表中的一行：

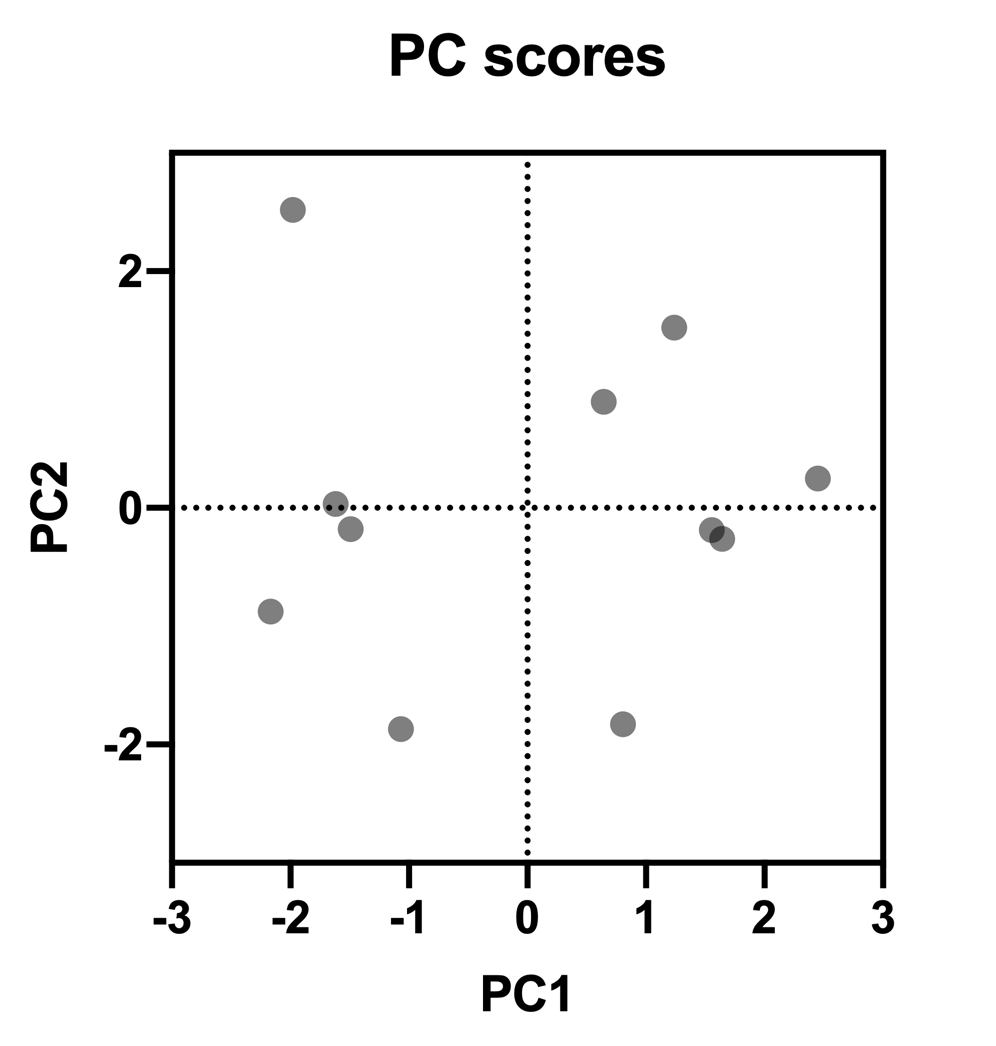
使用这种图表，通常可以观察到数据点群。本示例图表中，左半部分的所有点都对应原始数据中的第 1-5 行，而右半部分的点则对应数据中的第 6-11 行。

在具有两个以上选定成分的 PCA 中，研究不同成分组合（PC1 和 PC3、PC2 和 PC3 等）之间的关系有时非常有用。但是，请记住，第一个成分比第二个成分包含更多的 "信息"（以解释方差的形式），第二个成分比第三个成分包含更多的 "信息"，以此类推。因此，最有用的信息通常是在比较前几个分量的图表中发现的。