引言

该方程描述了配体与其受体或底物与酶之间交互作用的伪一阶关联动力学。在每个时间间隔内，有一部分未被占用的受体被占用。但随着时间的推移，未被占用的受体越来越少，因此结合的配体也越来越少，曲线也就趋于平稳。

输入数据

创建 XY 数据表。在 X 列中输入时间，在 Y 列中输入反应（结合、浓度......）。如果有多个实验条件，则将第一个条件放入 A 列，第二个条件放入 B 列，等等。

输入数据后，点击分析，选择非线性回归，选择指数方程面板，并选择单相关联。

考虑将 Y0 限制为常数零值

在这种情况下，应将参数 Y0 限定为等于零的常数。为此，请转到非线性回归对话框的 "约束"选项卡，将 Y0 旁边的下拉菜单设置为 "常数等于"，然后输入 0.0。这样做将迫使生成的曲线通过原点。

模型

Y=Y0 + (高原-Y0)*(1-exp(-K*x))

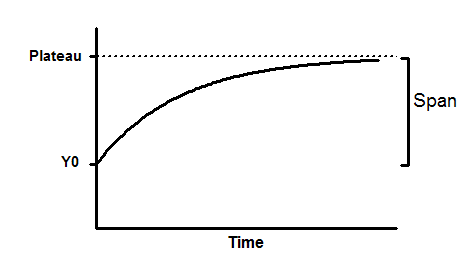
Y0是 X（时间）为零时的 Y 值。其单位与 Y 相同、

高原是无限时间时的 Y 值，单位与 Y 相同。

K是速率常数，用 X 轴时间单位的倒数表示。如果 X 以分钟为单位，则 K 以倒数分钟为单位。

Tau是时间常数，单位与 X 轴相同。其计算公式为 K 的倒数。

Half-time以 X 轴的时间单位表示。计算公式为 ln(2)/K。

跨度是 Y0 和高原之间的差值，单位与 Y 值相同。