引言

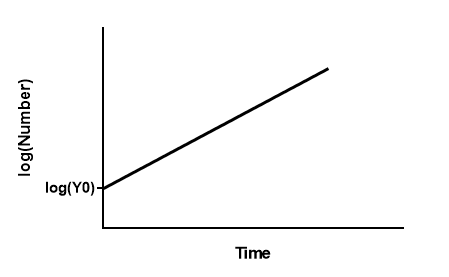
在指数增长的情况下，人口以恒定的加倍时间永远保持增长。如果将人口的对数绘制成 Y（而不是人口本身），那么图形就是线性的。 当您拟合指数模型时，您希望所有时间点的散点都大致相同。如果拟合的是浓度的对数而不是浓度，这一假设通常更有可能成立。

步骤

创建 XY 表。在 X 表中输入时间值，在 Y 表中输入群体值的对数。自然对数最常用于这类数据。如果使用其他对数（如 10 或 2），得到的曲线仍将是一条直线。但是，对参数的解读将是错误的（具体来说，只有在数据表中输入的 Y 值代表种群值的自然对数时，才能正确解读 Prism 报告的加倍时间）。

输入数据后，单击分析，选择非线性回归，选择生长方程面板，然后选择指数生长方程的对数。

考虑是否应将 logY0 限制为固定值。

模型

Y=logY0 + k*X

 

解读参数

logY0是与 Y 相同对数单位的起始人口数

k是速率常数（X 时间单位的倒数）。

加倍时间（DoublingTime ）是种群加倍所需的时间。计算公式为 ln(2)/k。

该生长方程与指数（马尔萨斯）增长之间的关系

如果使用自然对数对数据进行转换，那么本拟合方程中的 k 相当于指数（马尔萨斯）增长方程中的 k，这里的 logY0 相当于指数方程中 Y0 的对数。

但这两个 k 值通常不会完全相同。当所有时间点的数据围绕曲线的散度相同时，指数生长方程更为合适。当所有时间点上围绕直线的数据散度相同时，指数生长方程的对数更合适。