当许多独立的随机因素以相加的方式产生变异性时，就会出现高斯分布。本示例最能说明这一点。

想象一个非常简单的 "实验"。你用移液器移出一些水并称重。你的移液器本应输出 10 微升的水，但实际上随机输出了 9.5 到 10.5 微升的水。如果您移液一千次，并将结果绘制成频率分布直方图，它将如下图所示。

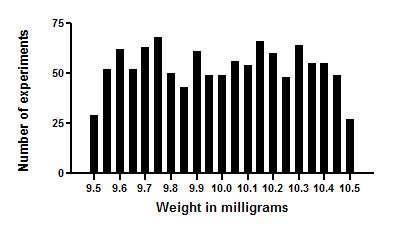
平均重量为 10 毫克，相当于 10 微升水的重量（至少在地球上是这样）。分布是扁平的，没有一丝高斯分布的迹象。

现在让我们把实验复杂化。我们移液两次，然后称量结果。现在的平均重量是 20 毫克。但你希望误差会在某些时候抵消。下图就是你得到的结果。

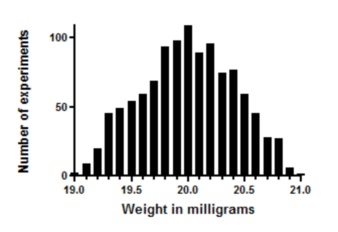
每个移液步骤都有一个固定的随机误差。把它们加起来，分布就不平了。本示例中，只有当两个移液步骤的误差基本一致时，才会得到接近 21 毫克的重量，而这种情况很少见。

现在，让我们将其扩展到十个移液步骤，看看总和的分布情况。

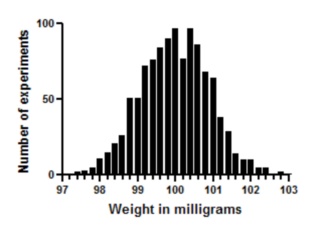
这种分布看起来很像理想的高斯分布。重复实验 15000 次，而不是 1000 次，你就更接近高斯分布了。

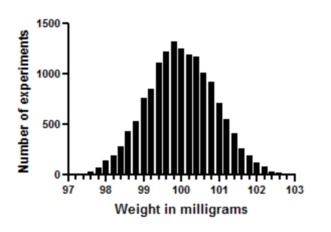
这个模拟演示了一个也可以用数学方法证明的原理。如果您的实验散点有许多来源，这些来源是相加的，权重几乎相等，而且样本量很大，那么散点就会近似于高斯分布。

高斯分布是一种数学理想。真正服从高斯分布的生物分布少之又少。高斯分布从负无穷延伸到正无穷。如果本示例中的权重真的服从高斯分布，那么权重为负的几率就会存在（尽管非常小）。因为权重不可能是负数，所以分布不可能完全是高斯分布。但它与高斯分布足够接近，因此可以使用假设为高斯分布的统计检验方法（如 t 检验和回归）。