什么是投影？

对于具有大量变异性的数据集，需要进行降维处理，以便更容易理解数据内部的关系，或从数据中生成可用于可靠预测未来观测结果的模型。实现降维的一种方法是 "投影"。幸运的是，即使不熟悉它的名字，我们对这个概念也都不陌生。

在上一节中，我们考虑了使用 "三维"图表来沿着三个独立的维度（三个变异性用作垂直轴）显示数据。不过，这些 "三维"图表的特点在于，它们实际上并不包括三个垂直轴，而只是代表三个轴。这些图形呈现在纸张或电脑显示器上，每张纸或显示器都是平面的，只有两个维度（长度和宽度，但没有深度）。这些 "三维"图形看起来只有第三个空间维度，而实际上只有两个。这一点看似显而易见，但却是与降维相关的一个重要概念。

这些 "三维"图形的实际情况是，由三维（三个变异性）描述的信息被投射到了二维空间中。幸运的是，我们（人类）的大脑非常擅长解读三维数据向二维的投影。每当我们看到一张照片或观看一部电影时，我们都在解读三维信息的二维投影，而且我们能很好地理解这些图像中隐含的 "深度"信息，尽管并没有任何 "深度"信息。

投影到轴上

为了让本节的其他概念更容易理解，让我们考虑一下仅由两个变量（之前的变异性 A 和 B）组成的简单数据集。这里又是数据：

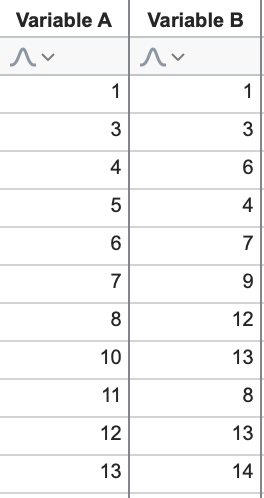
我们来看一个使用（二维）图表进行投影的本示例：

 

这是上述数据集中两个变异性变量的图形。将数据投影到 X 轴（变异性 A）上可能是这样的：

 

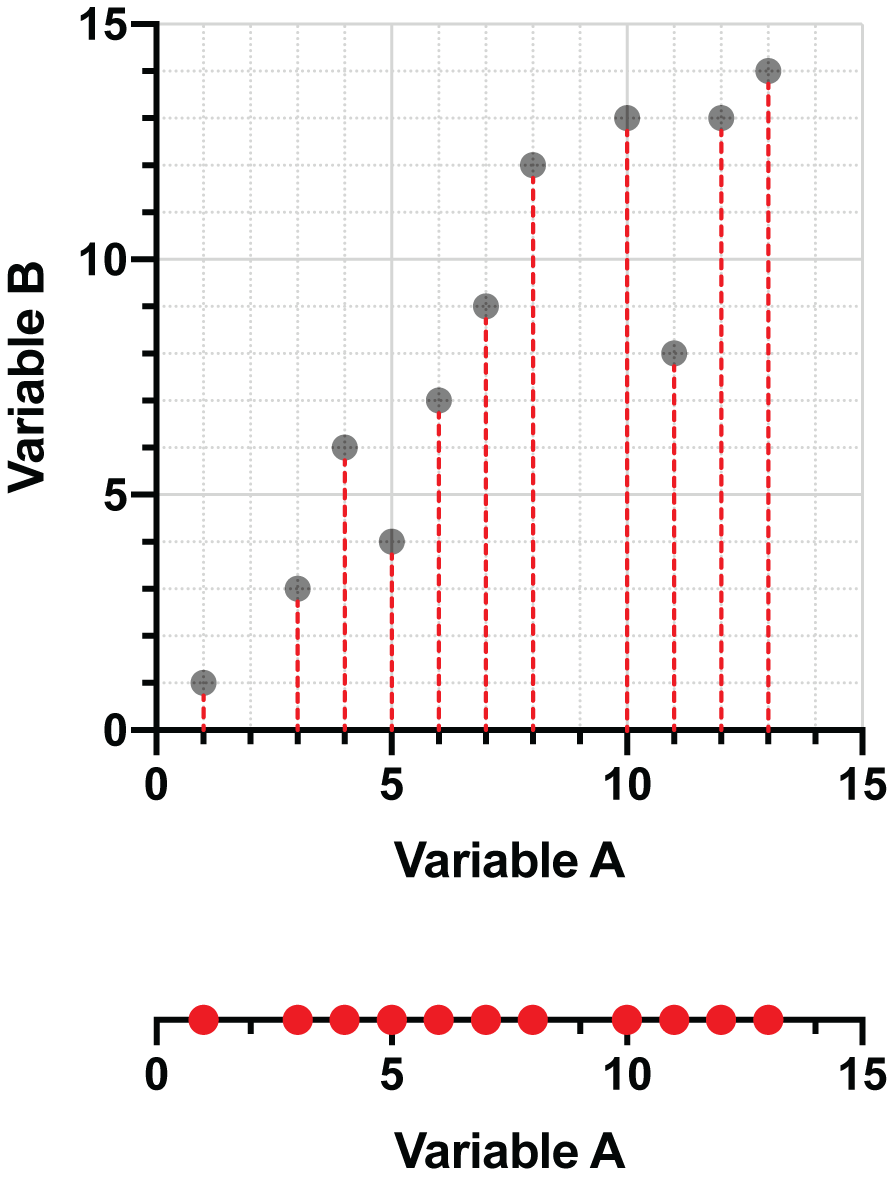
如果我们选择将数据点投影到 Y 轴（变量 B）上，最终会得到这样的图形：

 

 

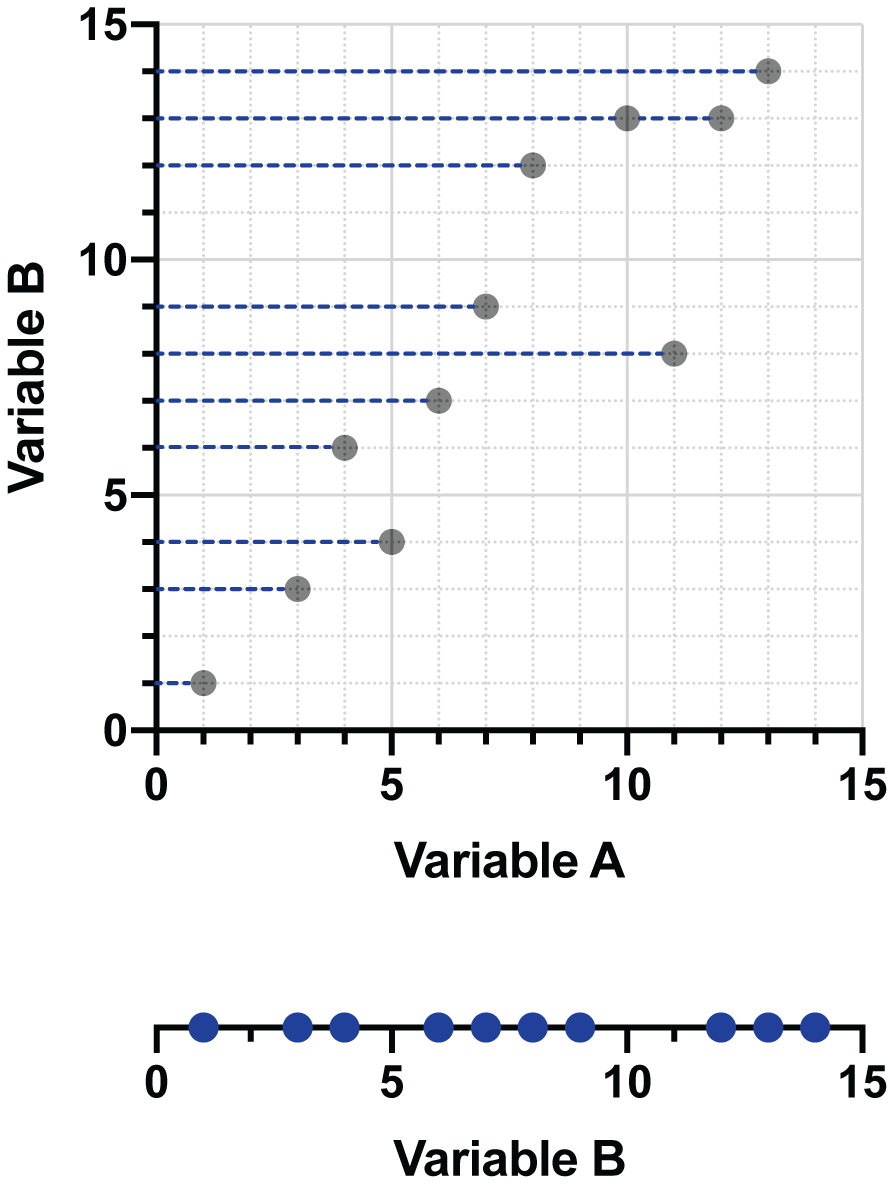
您可能已经意识到，通过这些投影，我们减少了描述数据所需的维数。在第一个本示例中，我们只需要变量 A 的值，就可以用一条简单的数线来表示这些投影数据。在第二个本示例中，我们最终得到的是变量 B 的值，我们可以再次将这些值表示在一条数线上（旋转后更易于阅读）。

投影到其他行

将数据投影到一个或其他坐标轴上，可以看出描述数据所需的维度减少了。不过，这也表明，无论采用哪种方法，都会丢失大量信息。投影到变量 A（X 轴）上时，会丢失变量 B 的信息，反之亦然。通常情况下，我们希望尽可能减少投影过程中丢失的信息量。因此，还有其他一些投影方法可以保留两个变异性的信息，其中一种可能大家都很熟悉。

线性回归是将点投影到直线上的一种极为常见的方法。一般来说，回归的方式是使点与直线之间的垂直距离平方和最小。请看下面两幅图：

 

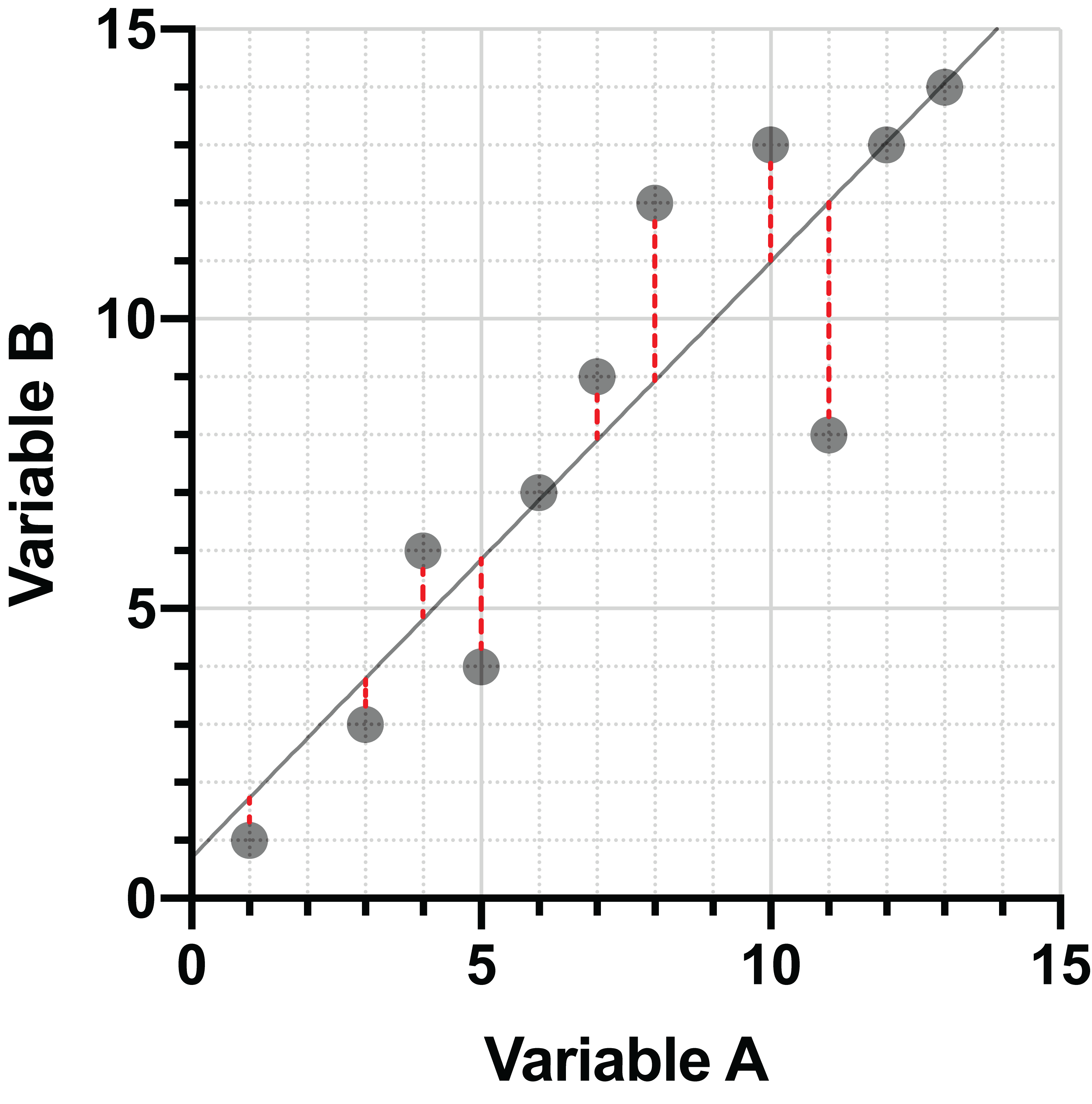
左图中，点被投影到拟合度较差的直线上，点与直线之间的垂直距离较大。右图中，垂直距离已经最小化，这是该数据的拟合优度最好的直线。

在标准回归中，数据沿 Y 方向（垂直）投影到直线上，这些距离被最小化。不过，也可以使用其他技术来投影数据。本示例采用 X 方向（水平）投影。这些距离的最小化会产生一条略有不同的直线：

 

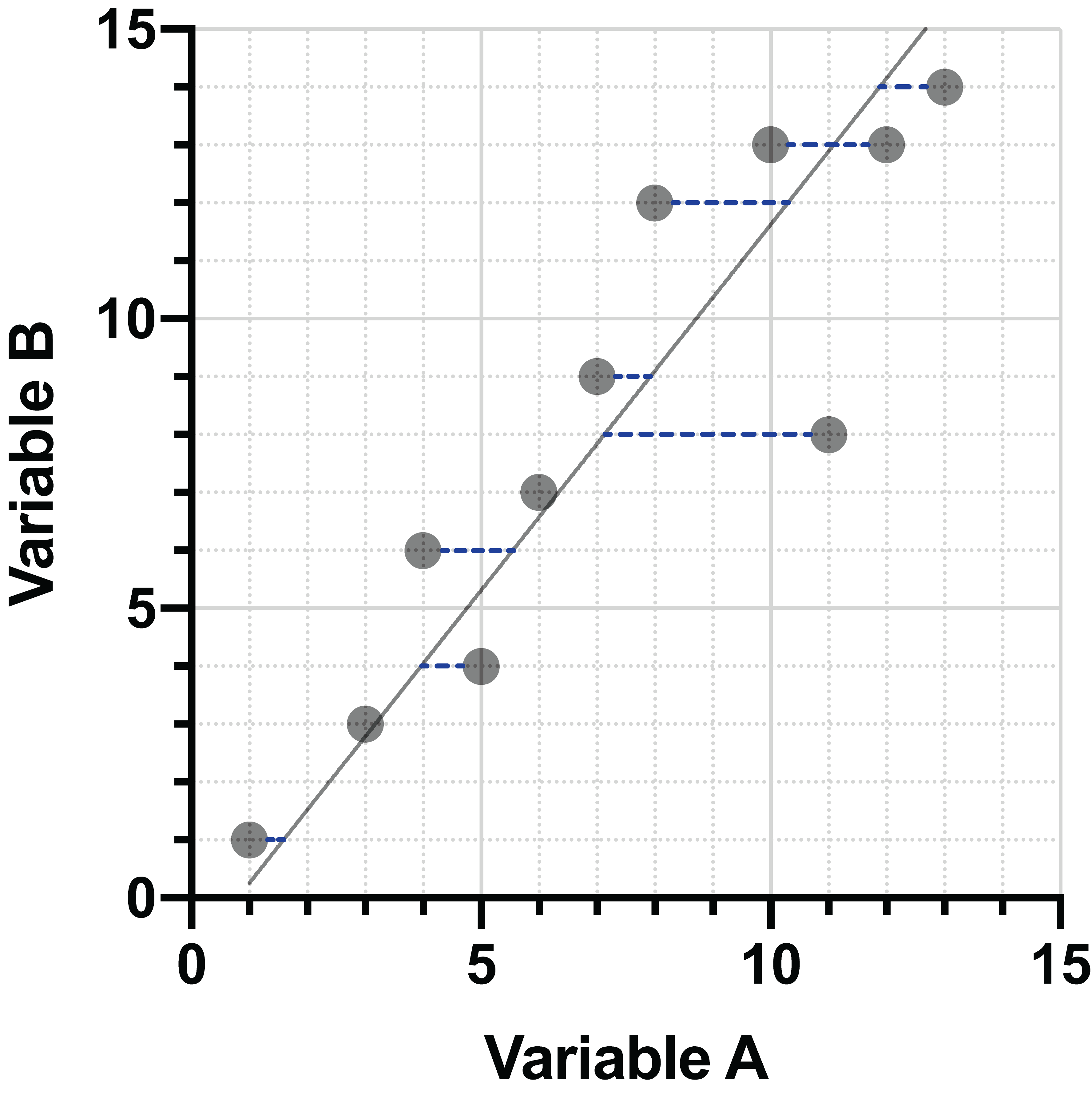
将数据投影到直线上的另一种方法是同时最小化两个方向的距离。我们将使用与之前相同的数据，但在向前推进之前，我们要对其进行一些变换。这些变换不仅能让你直观地了解最后一种投影方法与其他两种方法的比较，而且由于主成分的定义方式，它们在进行 PCA 时也很重要。这将在另一节中详细讨论。

下面是我们的原始数据：

我们将对这些数据进行标准化处理。为此，我们首先要计算每个变量的平均值和标准偏差。然后，对于变量中的每个值，减去该变量的平均值，再除以其标准偏差（有时也称为值的 Z 分数）。对于这些数据，标准化后的数值如下（四舍五入）：

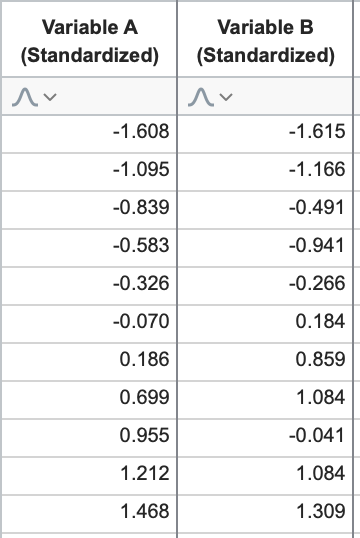
关于已经标准化的变量，有一个重要的事实需要注意，它们的均值总是 0，标准偏差总是 1。 让我们在图表上看看这些标准化数据。

 

总的来说，标准化数据的图表看起来与原始数据的图表非常相似，只是进行了移动，使点云的 "中心"位于原点（0,0）。请注意，X 和 Y 方向的数据比例也发生了变化，但由于两组数据的标准偏差相似（变量 A 为 3.90，变量 B 为 4.45），因此散点图的整体形状并没有发生太大变化。

利用标准化数据，现在让我们看看如何将这些点投影到一条直线上，同时使点与直线之间的水平距离和垂直距离最小化。由于我们对数据进行了标准化处理（即 X 方向和 Y 方向的方差相同），这就等同于最小化点与直线之间的垂直距离：

 

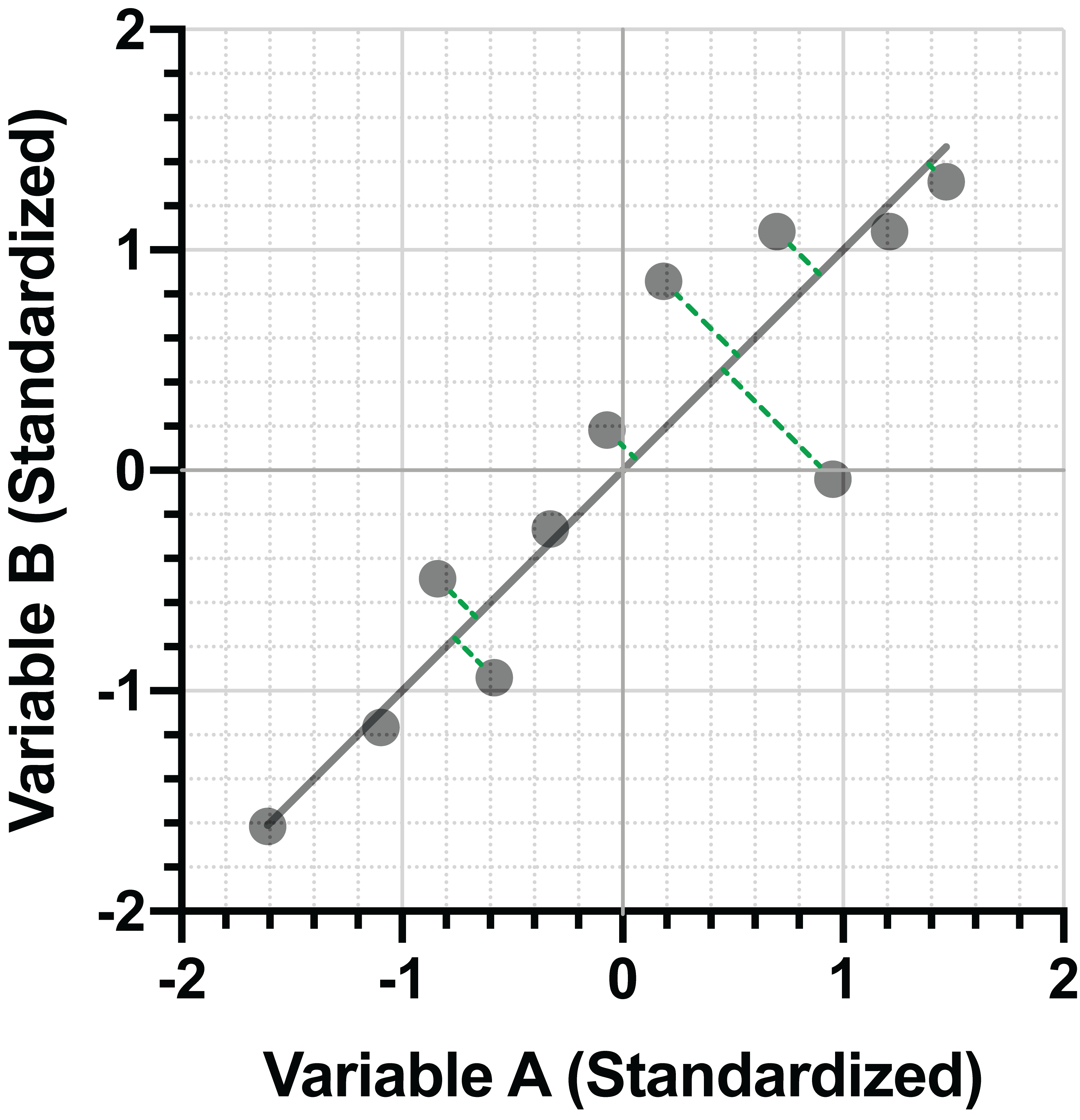
如果我们将这条直线与用最小化点与直线之间的垂直距离（红色）或水平距离（蓝色）拟合的直线进行比较，我们会发现，最小化垂直距离（绿色）的直线位于正中间：

 

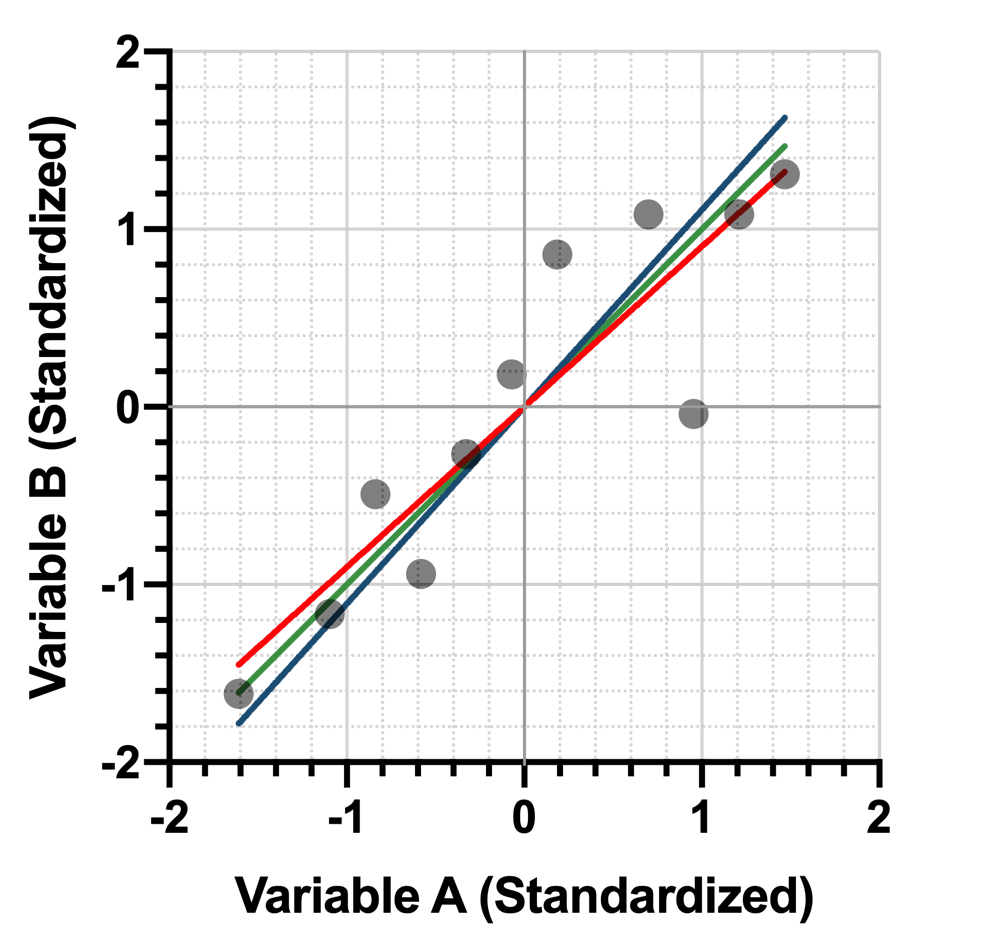
回报

那么，我们为什么要对数据进行投影，并使用不同的线进行投影呢？事实证明，在使用标准化数据时，通过最小化点与直线之间的垂直距离来拟合标准化数据的直线，也能最大化拟合直线上投影数据的方差。这意味着同时使用这一过程

•将数据投影到拟合线上所损失的信息量最小化

•使投影数据在拟合线上的方差最大化

为了更清楚地说明这一点，我们再做一个图形比较。这里同样是通过最小化标准化数据点与直线之间的垂直距离，将投影拟合到直线上：

 

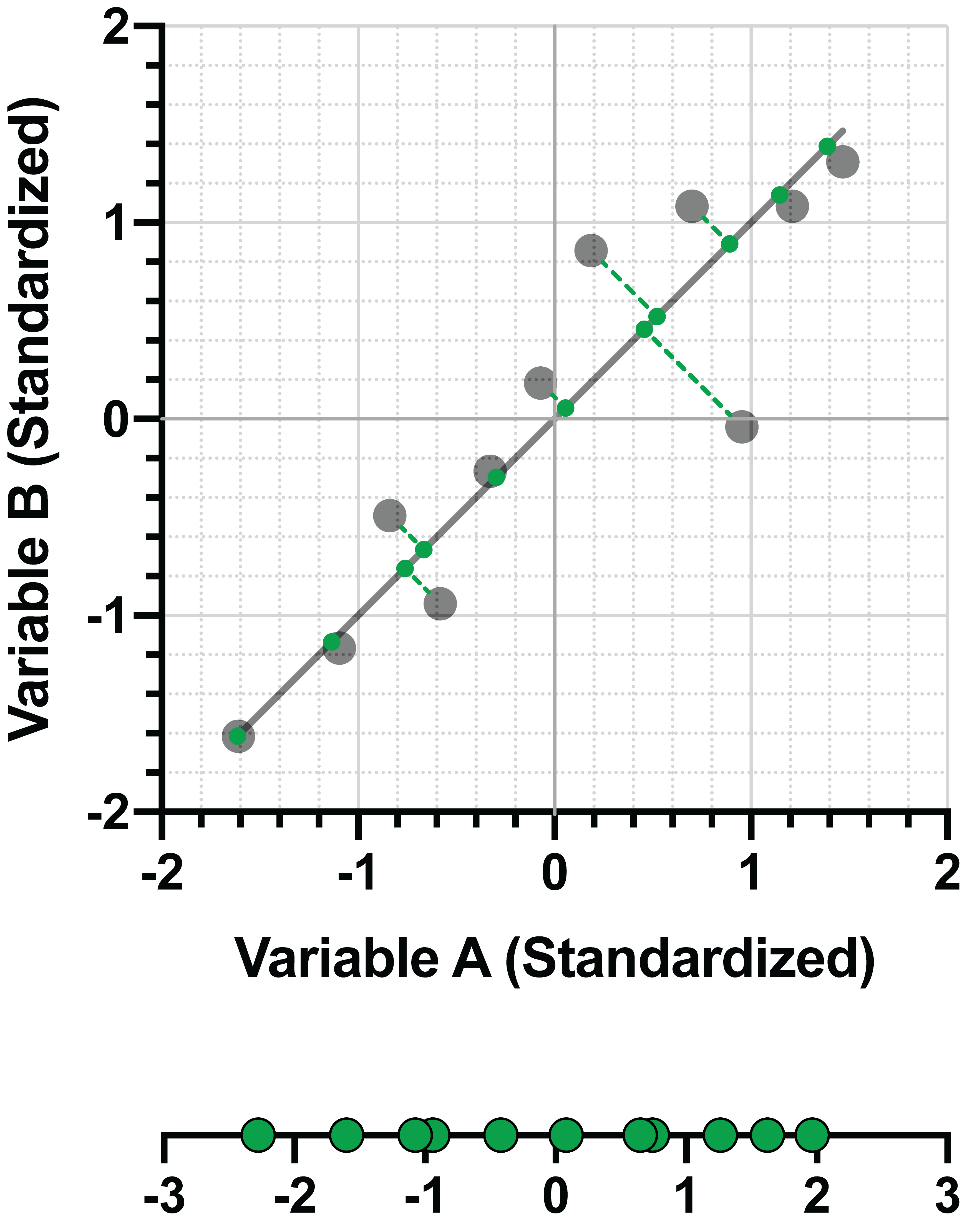
现在比较一下垂直投影到不同直线上的相同数据的方差（扩散）：

 

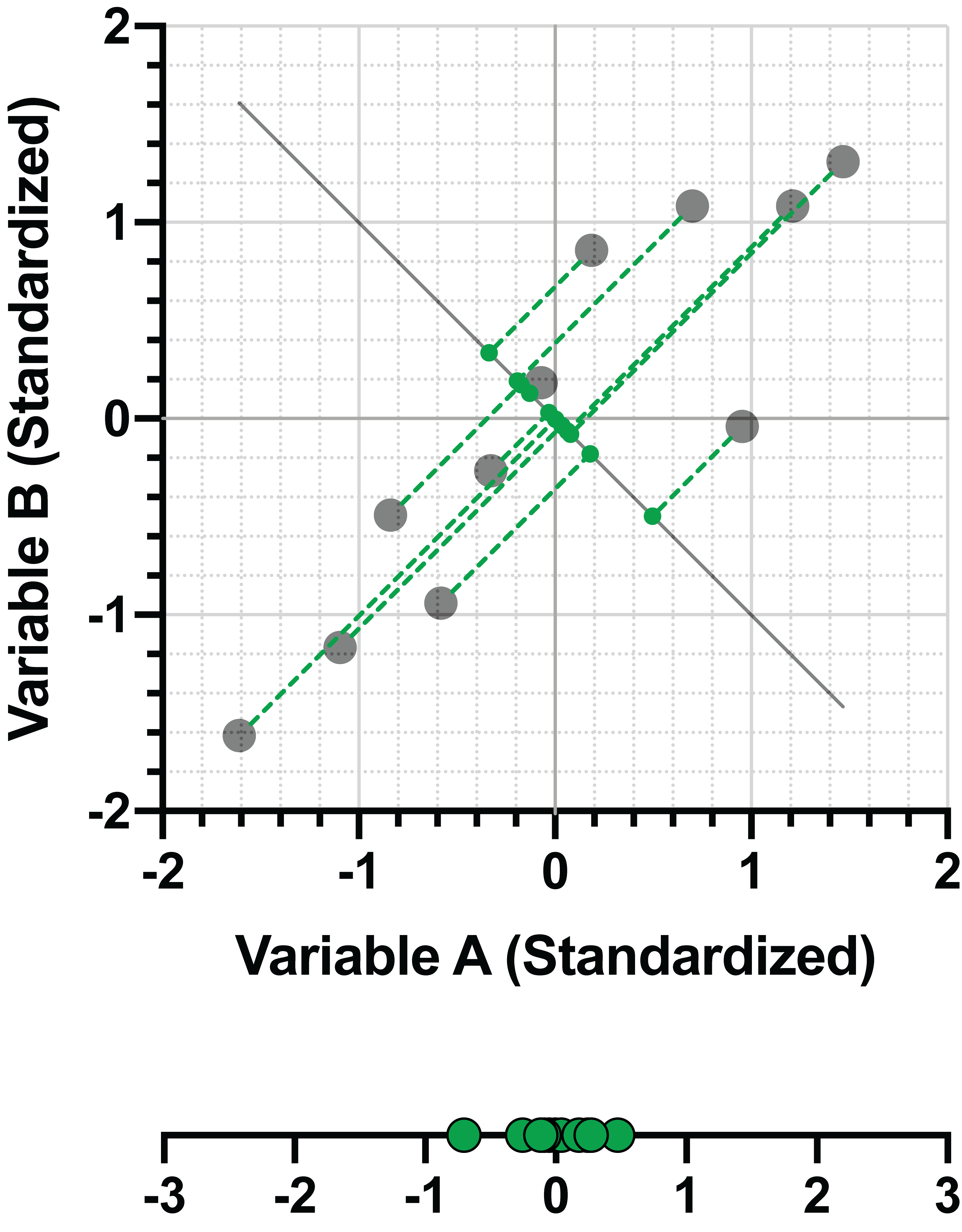
在第二张图中，很明显各点与直线之间的距离要比前一张图大很多，而且投影数据在直线上的聚类也更紧密。令人惊讶的是，将数据点与直线之间的垂直距离最小化，就等于将直线上投影数据的方差最大化。更重要的是，这正是 PCA 所要做的：通过将数据投射到较少的维度上，解释数据中最大的方差。当然，PCA 是在变量较多的情况下实现这一目的的。如果只有两个变异性变量，就没有必要降维。